2. 確率と確率分布
A. 確率
a. 標本空間、事象
b. 確率、条件付き確率 (2015 60)
・順列 nPk=n(n-1) (n-2)
(n-3)…(n-k+1)
・組合せ nCk=nPk÷k!
c. 離散型確率変数、連続型確率変数
d. 大数の法則、中心極限定理
B. 確率分布
a. 離散型確率分布、連続型確率分布
b. 自由度
c. 二項分布、ポアソン分布、正規分布、t分布、χ2 分布、F 分布 (2017 28、2013 63)
○離散型
:「二項分布」「ポアソン分布」
○連続型
:「正規分布」「t分布」「F分布」「ラプラス分布」「χ2 分布」
d. 期待値、分散
○確率密度関数 (2017 27)
連続確率変数の確率分布を規定する関数を確率密度関数
確率変数X が連続的な値をとる連続確率変数であるときに X がある範囲 [a, b] をとる確率を P とした場合,その確率を与える以下の関数 f(x) を確率密度関数という。
○確率質量関数(2017 27)
離散確率変数の確率分布を規定する関数を確率質量関数
確率変数X が離散的な値をとる離散確率変数であるときに X が x をとる確率を P とする場合,その確率を与える以下の関数 f(x) を確率質量関数という。単に,確率関数という場合もある。
3. 推定、検定
A. 推定
a. 点推定、区間推定 (2014 64)
・点推定
:平均値などを一つの値で推定すること
・区間推定
:平均値などをある区間でもって推定すること(2014 64)
b. 信頼区間
:平均値などの値がある確率でその区間にあることで、その確率を信頼水準という
信頼水準を大きくすると(外れる確率が小さくすると)、信頼区間は広がり(推定が甘くなる)
標本数が大きい:信頼区間の幅が狭い(精度が高い
c. 一致性、不偏性、有効性
d. モーメント法、最尤法
e. ベイズ推定
f. モンテカルロ法
g. ブートストラップ法
B. 統計的仮説検定
a. 帰無仮説、対立仮説 (2013 63)
立証したい命題H1:対立仮説
H1を否定した命題H0:帰無仮説
帰無仮説が成立しているが棄却する確率α:有意水準
〇統計的仮説検定の手順
確率1-α=0.95or0.99(95%or99%)で判定 α:有意水準
↓有り得ない ↓有り得る
仮説H0と矛盾する 仮説H0と矛盾しない
↓ ↓
H0を棄却(否定) H0を保留(肯定ではない)
↓ ↓
確率1-α(95%or99%)で 確率1-α(95%or99%)でしか
H1は正しい(A≠B)といえる H0は正しい(A=B)と言えない
↓
H1は正しい(A≠B)とは言えない
*確率5%(1%)は間違っている可能性もあることに留意する
b. p値〈有意確率〉、αエラー〈第一種過誤〉、βエラー〈第二種過誤〉、検出力〈検定力〉
|
|
母集団の真の状態 |
||
|
真 |
偽 |
||
|
下した結論 |
採択 |
正 |
誤(第2種過誤)過誤確率β |
|
棄却 |
誤(第1種過誤)過誤確率α |
正 |
|
α:有意水準
小さい方が良いが、棄却が難しくなる
1-β:検出力
間違った仮説を正しく棄却する確率で、標本数の調整によって小さくした方が良い
c. 両側検定、片側検定
d. パラメトリック検定、ノンパラメトリック検定
・パラメトリック検定
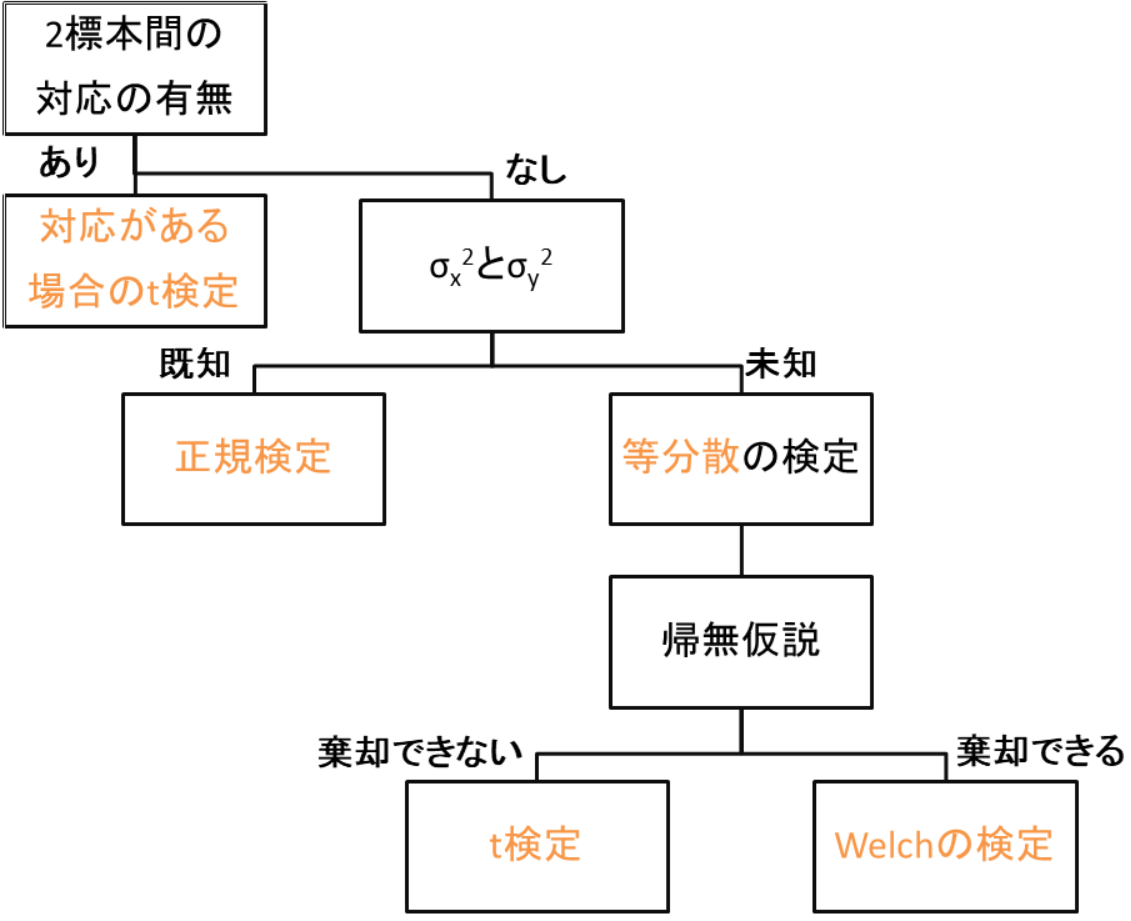
データが正規分布に従う → 以下のフローチャートで平均値の差の検定を開始
・ノンパラメトリック検定 (2016 19、2013 63)
データが正規分布に従わない
Ex)Steel-Dwass、2群ごとにMann-WhitneyのU検定、
2条件ごとにWilcoxonの符号順位検定を適用後Bonferroniの調整
e. 対応のない検定、対応のある検定
f. 平均値の検定、分散の検定、比率の検定 (2013 63)
対応有:対応がある場合のt-検定
対応無、分散が等しい:t-検定
対応無、分散が等しくない:Welch検定
g. 適合度の検定:χ2 検定
h. 等分散の検定:F-検定
i. 独立性の検定:χ2 検定
j. 平均値の差の検定、比率の差の検定
k. 2 群間の検定、多群間の検定
*バートレット検定
複数の群それぞれの分散の均一性の検定
*フリードマン検定
データの正規性を考慮せず、2変数の3つ以上のグループ差の検定
4. 回帰分析
A. 単回帰分析
a. 説明変数〈独立変数、内的基準〉、目的変数〈従属変数、基準変数〉、潜在変数〈交絡因子〉
b. 線形回帰分析 c. 共分散 d. 相関係数 e. ロジスティック回帰分析
B. 多変量解析
a. 重回帰分析
b. 主成分分析 (2016 20)
相関のある多数の変数から、相関のない少数で全体のばらつきを最もよく表す主成分、と呼ばれる変数を合成する多変量解析の手法。データの次元を削減するために用いられる。
Karhunen-Loéve 変換(KL変換):元の画素値を各主成分に変換する式の直交変換
c. 因子分析 d. 数量化理論 e. クラスター分析 f. その他
5. 医学統計
A. 人口統計
B. 健康指標(生命表、指標)
C. 生存率算出規約
D. 生存時間解析
a. イベント、観察時間
b. 生存関数、ハザード関数
c. カプラン・マイヤー法
d. コックス回帰分析
e. ログランク検定
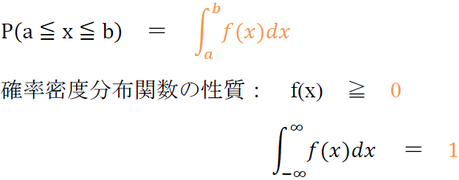
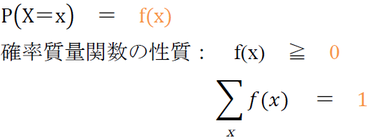



コメント