2.原子、原子核
C. 核反応
a. 実験室系と重心系
・実験室系
実験室に対して静止した座標系
・重心系
重心に対して静止した座標系(重心と一緒に動くような座標系)
b. 散乱、捕獲
c. 核反応とQ 値
(2016 08、2015 06、2012 03)
○核反応式:A(x,y)B
A:標的原子核 x:入射粒子
y:放出粒子 B:反跳原子核
○Q値
核反応前後の質量欠損をエネルギーに換算した値
Q = (MA+Mx)×C2 -(MB+My)×C2
Q値>0ならば発熱反応で、閾エネルギーはない
Q値<0ならば吸熱反応で、閾エネルギーはある
閾値Emin= -Q ×(MA+Mx)÷MA
d. 発熱反応、吸熱反応 e. しきいエネルギー f. 核破砕
D. 核磁気、スピン
○ボソン (ボース統計に従う粒子:ボース粒子)
・ゲージ粒子
素粒子間の相互作用(力)を伝え運ぶ粒子
スピンはすべて1となる
― 光子(フォトン)
- 電磁相互作用を媒介する
ガンマ線の正体であるためγで表されることが多い
― ウィークボソン
- 弱い相互作用を媒介する
質量を持つ
― グルーオン
- 強い相互作用を媒介する
カラーSU(3)があり、23の数、つまり八種類存在する
― 重力子(グラビトン)
- 重力を媒介する(未発見)
・ヒッグス粒子
素粒子に質量を与える
スピンはすべて0となる
○フェルミオン (フェルミ統計に従う粒子:フェルミ粒子)
・フェルミオン
物質を構成する粒子
スピンはすべて1/2となる
クォークとレプトンに大きく分けられ、更にそれぞれが二系列に分けられ、三世代ずつの計6種類が発見されている
傾向として、世代数が大きいほど質量が大きいとされている
― クォーク
強い相互作用をする。ハドロンの構成要素とされる。
-上系列(アップ、チャーム、トップクォーク)
- 電荷+2/3を持ち、それぞれに反粒子が存在する。
-下系列(ダウン、ストレンジ、ボトムクォーク)
- 電荷−1/3を持ち、それぞれに反粒子が存在する。
― レプトン
強い相互作用をしない。
-ニュートリノ(電子、ミュー、タウニュートリノ)
- 電荷をもたない。反粒子の存在が必然ではない。
-荷電レプトン(電子、ミュー粒子、タウ粒子)
- 電荷−1を持ち、それぞれに反粒子が存在する。
a. スピン
(2016 10、2015 05 08)
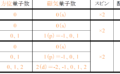
| 分類 | 記号 | 名称 | 電荷 | ★スピン | 質量 |
| ハドロン バリオン | P | 陽子 | +1 | 1/2 | 1 |
| ハドロン バリオン | n | 中性子 | 0 | 1/2 | 1.001 |
| ハドロン メソン | π+ | パイ中間子 | +1 | 0 | 0.148 |
| ハドロン メソン | π0 | パイ中間子 | 0 | 0 | 0.143 |
| ハドロン メソン | π- | パイ中間子 | -1 | 0 | 0.148 |
| レプトン | νe | 電子ニュートリノ | 0 | 1/2 | 0 |
| レプトン | e | 電子 | -1 | 1/2 | 0.0005 |
| ゲージボソン | r | フォトン | - | 1 | 0 |
*質量数が偶数なら核スピンは整数、奇数なら半奇数(半奇整数・半整数)
質量数が偶数で、原子番号が偶数なら核スピンは0
*パウリの排他原理 (2017 05、2014 1)
2つ以上のフェルミ粒子は同一の量子状態を占めることはできない
b. ゼーマン効果 c. 磁化率 d. 歳差運動 e. 磁化ベクトル
E. 放射性壊変
a. 壊変定数、平均寿命、半減期
○放射能A (2016 09)
A = -dN/dt = λ×N
λ:壊変定数 N:原子数
・壊変定数λ (2016 09)
λ = ln(2)/T = 0.693/T
・分岐比 (2016 09)
λ=λ1+λ2+λ3+……
λ1,λ2,λ3:部分壊変定数
分岐比 → λ1:λ2=T2:T1
・平均寿命τ (2016 03 09)
τ=1/λ=1.44×T
b. 親核種と娘核種の関係 c. 過渡平衡、永続平衡
・放射平衡 (2014 05)
$$A_{ 2 }=\frac { λ_{ 2 } }{ λ_{ 2 }-λ_{ 1 } } ×A_{ 1 }^{ 0 }×(e^{ -λ_{ 1 }t }-e^{ -λ_{ 2 }t })+A_{ 2 }^{ 0 }×e^{ -λ_{ 2 }t }$$
$$N_{ 2 }=\frac { λ_{ 1 } }{ λ_{ 2 }-λ_{ 1 } } ×N_{ 1 }^{ 0 }×(e^{ -λ_{ 1 }t }-e^{ -λ_{ 2 }t })+N_{ 2 }^{ 0 }×e^{ -λ_{ 2 }t }$$
・過渡平衡 (2016 09)
成立条件:λ1<λ2、T1>T2
$$A_{ 2 }=\frac { λ_{ 2 } }{ λ_{ 2 }-λ_{ 1 } } ×A_{ 1 }^{ 0 }$$
$$N_{ 2 }=\frac { λ_{ 1 } }{ λ_{ 2 }-λ_{ 1 } } ×N_{ 1 }^{ 0 }$$
$$Tmax=\frac { 1 }{ λ_{ 2 }-λ_{ 1 } } ×ln\frac { λ_{ 2 } }{ λ_{ 1 } } $$
・永続平衡
成立条件:λ1<<λ2、T1>>T2
$$A_{ 2 }=A_{ 1 }^{ 0 }$$
$$N_{ 2 }=\frac { λ_{ 1 } }{ λ_{ 2 } } ×N_{ 1 }^{ 0 }$$
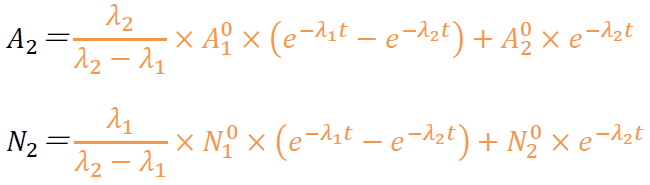

コメント