C. 電子線と物質との相互作用
a. 衝突、散乱
b. 制動放射
○制動X線の発生
(2014 24、2013 22、2012 21)
・単位時間の発生強度I$$I=K×I×Z×{ V }^{ 2 }$$
・制動放射線の発生効率η$$η=K×Z×V[%]$$
*診断領域ではηは1%未満である。
K:定数(1.1×10-9)
I:管電流
Z:ターゲットの原子番号
V:管電圧
○制動X線の強度分布(角度)
(2017 12、2014 07)
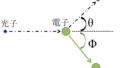
・ゾンマーフェルトの理論式I(θ)$$I(θ)=A-\frac { { sin }^{ 2 }θ }{ { (1-βcosθ) }^{ 6 } } $$
θ:ターゲットへ入射した電子の進行方向を0°とした角度
・入射電子のエネルギーが増加した場合(10MeV以上)
βが1に近づく → θ=0°(前方)の強度が増加
・入射電子のエネルギーが減少した場合(30~150keV程度)
βが0に近づく → θ=90°(側方)の強度が増加
○管電圧と制動放射線の最大エネルギーの関係
・デュエンハントの法則 (2013 22)
加速電子のエネルギーE=e×V
V:X線管電圧[kV]
また、eV = hν = hC / λ
1eV=1.6×10^-19[J]
h=6.6×10^-34[Jsec]
C=3.0×10^8[m/sec]より
eV[kV]= Emax = hνmax
= hC / λmin
= 12.4 / λmin [Å]
*Å=10–10[m]
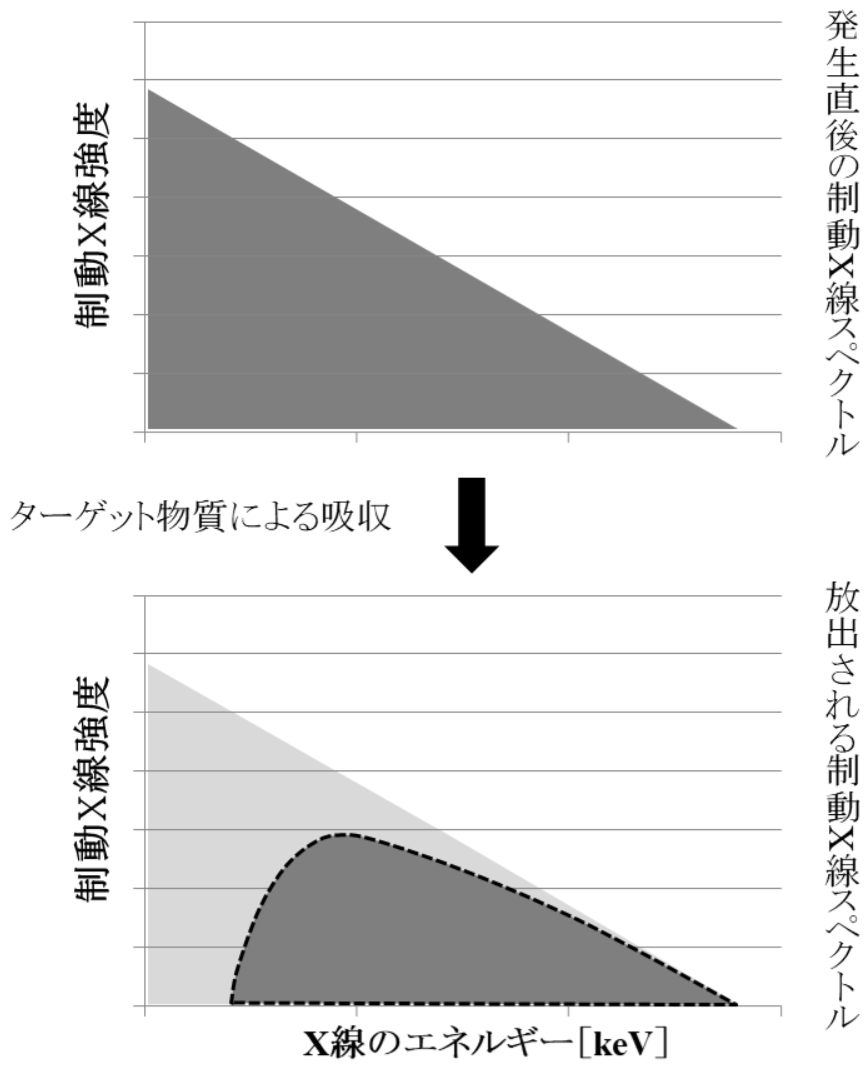
○ターゲットでの減弱前の制動X線

・クラマースの式 (2014 21)
光子エネルギーE×光子数N = k ×(Emax-E)
k:1.1×10-9
c. シンクロトロン放射
d. チェレンコフ放射
(2017 12、2013 08)
・荷電粒子が透明な誘電物質中(屈折率n)を通過するとき、物質中での光の速度(c/n)を超えた速度(v)で移動した場合に、分極によって位相が重なり、可視光(青色)が放出される現象
屈折率nの大きい物質で発生する
発生時間が非常に短く、シンチレーションの発生よりも短い
・電子の場合:水中で0.26MeV以上で発生
・臨界エネルギー:n(V/C)≧1
・チェレンコフ光と荷電粒子のなす角θ
cosθ= c/n ÷ v

e. 電子対消滅
○陽電子(ポジトロン)
(2015 08)
阻止能や飛程は電子と同じ
停止時に電子と結合
→ ポジトロニウムの形成
→ 消滅γ線(511keV)を2本以上放出する
*電子がない(真空中など)と安定する
f. 飛程
(2016 12、2017 15)
・連続減速近似(CSDA)で、エネルギー損失の揺らぎを無視し、電子は阻止能で単位長さ当たり平均エネルギー損失をすると仮定すると、電子の飛程を計算することができる。
・電子線の飛程
R = 0.5E‐0.3[cm](E=5~50MeV)
= 0.5E[g・cm-2](E>0.8MeV)
・質量が小さいため、散乱を受ける
g. 阻止能
(2016 13 、2017 12)
・阻止能:単位量当たりのエネルギー損失
・全線阻止能S=Scol+Srad
・線阻止能S:単位長さ当たりのエネルギー損失[MeV/mm]
・質量阻止能S/ρ:線阻止能を密度ρで割った値


○衝突阻止能
(2017 12、2016 13、2015 09)
・線衝突阻止能Scolは密度に比例する$$Scol∝\frac { N×Z }{ mv^{ 2 } } =\frac { ρ×Z }{ mv^{ 2 }×A } $$
・質量衝突阻止能Scol /ρ $$Scol/ρ∝\frac { 1 }{ mv^{ 2 } } =\frac { Z }{ A } $$
N:単位体積あたりの原子数$$N=\frac { ρ×N_{ A } }{ A } $$
ρ:密度 NA:アボガドロ数
Z:原子番号 A:物質の質量
m:電子の質量 v:電子の速度
・Z/Aの値は物質によって変化しない(≒0.5)ため、S/ρは物質の種類に依らない
*10MeV以上の場合は密度効果を考慮する必要がある
*電子の衝突損失
・電子のエネルギーEe<<電子の静止エネルギー
:Scol → 大きくなる
・電子のエネルギーEe>>2×電子の静止エネルギー
:Scol → 大きくなる
・電子のエネルギーEe=2×電子の静止エネルギー
:Scol → 最小付近
・(電子のエネルギーEe<100eV
:Scol → エネルギーの低下とともに小さくなる)
・後方散乱
(2014 07)
・多重散乱により起こり、薄い試料等での測定に影響を与える
線源支持体が厚い程、原子番号が高い程、影響が大きい(正比例ではなく飽和係数がある)
○放射阻止能
・線放射阻止能Srad
Srad ∝ N×Z2×(E+mc2)
= Z/A×ρ×Z×(E+mc2)
・質量放射阻止能Srad/ρ
Srad/ρ ∝ Z/A×Z×(E+mc2)
Z/Aの値は物質によって変化しないため、原子番号に依存する
○電子の放射損失と衝突損失の比
Srad/Scol = (E+0.511)× Z ÷ 820
E:電子のエネルギー[MeV]
Z:物質の原子番号
・臨界エネルギー:Srad=Scolとなるエネルギー
・電子の水/空気質量阻止能:深部ほど大きくなる
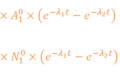
コメント
[…] → 電子線と物質との相互作用へ […]