1.基礎物理
B. 電磁気学
a. 電場
○同心球状電荷分布による電場 (2015 03)
外部電位E =(Q1+Q2)/(4πε0c)
内部電位E =(1/a-1/b+1/c×Q1/4πε0c+Q2/4πε0c
b. 磁場
○力の向き
・右ネジの法則 (2016 01)
直線電流がつくる磁場は下向きで時計回り
c. 電磁誘導 d. マクスウェル方程式 e. 電磁場のエネルギー f. 導体に伴う静電場 g. 回路
C. 熱力学・統計力学
a. 温度と状態方程式 b. 熱力学的諸過程 c. 平衡条件と巨視的状態量 d. 量子統計力学
D. 量子力学
○量子力学的運動量
・運動量演算子Px
$$Px=-iħ\frac { \partial }{ \partial x } $$
ħ:ディラック定数、ħ =h/2π
∂:偏微分
i:虚数
・演算子の交換関係 (2016 02)
{A 、B } = A B -A B = 0 :可換
{A 、B } = A B -A B ≠ 0 :非可換
演算子が可換ならば,同時にこれらの確定値(固有値)をとる状態(固有関数)が存在する
不確定性関係:位置と運動量は同時に決まらず,非可換である
a. 前期量子論
b. シュレーディンガー(波動)方程式
○波動関数(波動関数の解) (2015 01)
・一価関数、連続関数、有限関数でなければならない
・絶対値の二乗が確率密度関数
・時間に依存しない波動方程式の解
→エネルギー固有状態(離散的なスペクトル)
束縛状態の波動関数は遠方で 0 になる
ポテンシャルが無限大になるところでは,波動関数は 0 になる
エネルギー固有値が無限遠方におけるポテンシャルの値より小さいとき(E<V (±∞)),
エネルギーは離散的スペクトルをもち,逆の場合は連続的スペクトルをもつ
・エネルギー固有値 En=ħω(n+1/2) (n=1,2,3…) (2017 01)
n=0 :零点エネルギー
最も小さいエネルギー固有値:基底状態(偶関数)
n=1,2,3… :n=1 第一励起状態(奇関数)
n=2 第二励起状態 (偶関数),…
c. 近似解法
d. 散乱問題
○平均自由行程 (2016 04、2013 07)
光子や粒子が散乱することなく進むことのできる距離の平均値
平均自由行程を運動すると、平均として必ず他の物質と1回相互作用を起こす
・平均自由行程λ
$$λ=\frac { 1 }{ \sqrt { 2 } ×n×σ }$$
2種類の気体a、bの場合のσ:(ra+rb)2π
n:数密度=1/相対速度v
σ:有効断面積
r:半径
・光子の平均自由行程λ = 1/μ
e. 相対論的量子力学 f. 基本粒子と複合粒子
g. 4 つの力
(2015 05)
| 4つの力 | 電磁相互作用 | 重力 | 弱い相互作用 | 強い相互作用 |
| 相対強度 | ~10-2 | ~10-39 | ~10-13 | 1 |
| 作用距離 | ∞ (1/距離^2に働く) | ∞ (1/距離^2に働く) | ほぼゼロ | 近接~10-15m |
| 例 | クーロン力 | 引力 | β壊変,μ粒子崩壊 | 核力 |
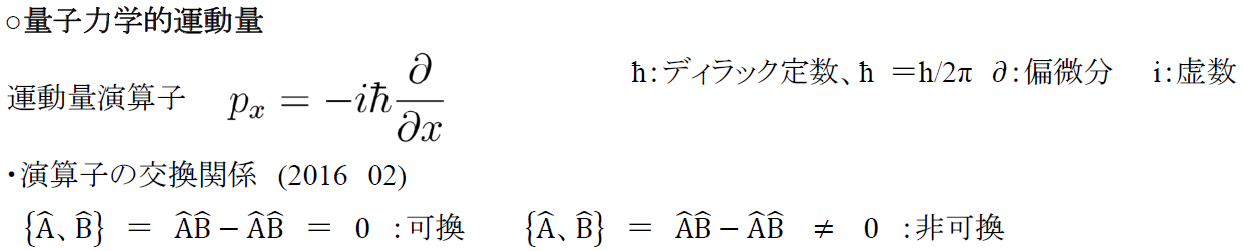


コメント